Nicolò Vignatavan - Linear equations and inequalities (ENG)
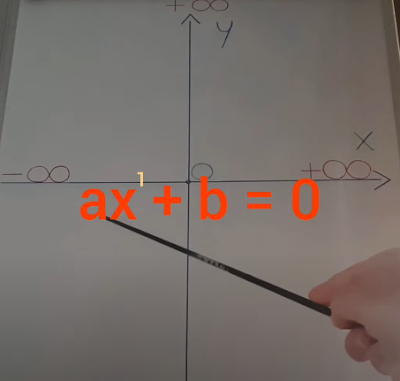
First degree linear equations and inequalities: the fundamental differences of representation on the Cartesian plane Nicolò Vignatavan -> Video A first degree equation is a polynomial equation whose degree or maximum exponential numerical value of the unknown or unknowns is 1, at the moment in which such polynomial, reduced to normal form, or rather, after having added all the similar monomials that made it up, is set equal to 0. If the unknown exponential appears to be of a numerical value greater than 1 in an equation reduced to normal form, then such equation will be defined of a higher degree than the first. The equations with one or more unknowns or variables (if they result to be reduced to normal form and of first degree) are called linear equations because their representation on the Cartesian plane graphically corresponds to straight lines; therefore linear geometric figures. The normal form in which a one variable (or unknown) fi